Fire-and-Forget MCMC Sampling (ligo.skymap.bayestar.ez_emcee)

ligo.skymap.bayestar.ez_emcee.ez_emcee(log_prob_fn, lo, hi, nindep=200, ntemps=10, nwalkers=None, nburnin=500, args=(), kwargs={}, **options)

Fire-and-forget MCMC sampling using ptemcee.Sampler, featuring automated convergence monitoring, progress tracking, and thinning.

The parameters are bounded in the finite interval described by lo and hi (including -np.inf and np.inf for half-infinite or infinite domains).

If run in an interactive terminal, live progress is shown including the current sample number, the total required number of samples, time elapsed and estimated time remaining, acceptance fraction, and autocorrelation length.

Sampling terminates when all chains have accumulated the requested number of independent samples.

Parameters:

log_prob_fncallable

The log probability function. It should take as its argument the parameter vector as an of length ndim, or if it is vectorized, a 2D array with ndim columns.

lolist, numpy.ndarray

List of lower limits of parameters, of length ndim.

hilist, numpy.ndarray

List of upper limits of parameters, of length ndim.

nindepint, optional

Minimum number of independent samples.

ntempsint, optional

Number of temperatures.

nwalkersint, optional

Number of walkers. The default is 4 times the number of dimensions.

nburninint, optional

Number of samples to discard during burn-in phase.

Returns:

chainnumpy.ndarray

The thinned and flattened posterior sample chain, with at least nindep * nwalkers rows and exactly ndim columns.

Other Parameters:

kwargs

Extra keyword arguments for ptemcee.Sampler. Tip: Consider setting the pool or vectorized keyword arguments in order to speed up likelihood evaluations.

Notes

The autocorrelation length, which has a complexity of \(O(N \log N)\) in the number of samples, is recalculated at geometrically progressing intervals so that its amortized complexity per sample is constant. (In simpler terms, as the chains grow longer and the autocorrelation length takes longer to compute, we update it less frequently so that it is never more expensive than sampling the chain in the first place.)

Examples

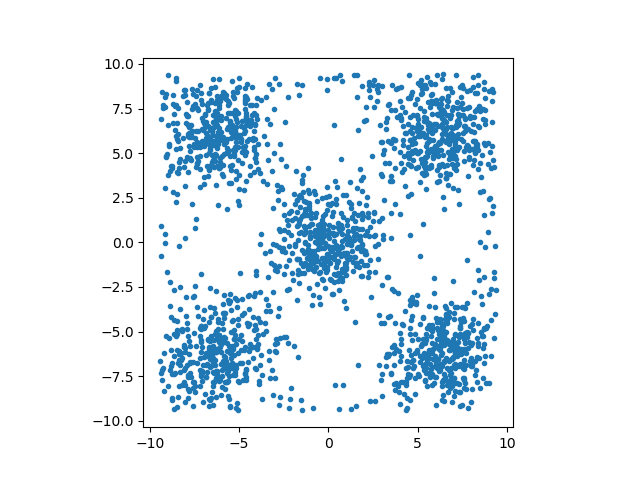
>>> from ligo.skymap.bayestar.ez_emcee import ez_emcee
>>> from matplotlib import pyplot as plt
>>> import numpy as np
>>>
>>> def log_prob(params):
...     """Eggbox function"""
...     return 5 * np.log((2 + np.cos(0.5 * params).prod(-1)))
...
>>> lo = [-3*np.pi, -3*np.pi]
>>> hi = [+3*np.pi, +3*np.pi]
>>> chain = ez_emcee(log_prob, lo, hi, vectorize=True)   
Sampling:  51%|██  | 8628/16820 [00:04<00:04, 1966.74it/s, accept=0.535, acl=62]
>>> plt.plot(chain[:, 0], chain[:, 1], '.')