This header file provides routines and structures to create and store window functions (also called a taper, lag window, or apodization function).
The Header Window.h package defines two data types, the REAL4Window and REAL8Window types. These are suitable for storing window function data, providing storage for a sequence of samples as well as metadata about the window such as the sum-of-squarse of the samples. The package also provides a collection of functions to construct a variety of pre-defined window functions.
The use of window functions in signal analysis is well documented in many places.
Definitions of most of the window functions can be found in Numerical Recipes [22] equations 13.4.13-13.4.15. Definitions of the remaining windows can be found in Spectral analysis for physical applications [21] Section 6.11. Definition of the Kaiser window can be found in Discrete-time Signal Processing by Oppenheim and Schafer, p.474.
These functions create or destroy a time-domain window function in a vector of specified length. If you wish to construct a custom window, call XLALCreateRectangularREAL8Window() (or the REAL4 version), then replace the samples inside it with your own, and update the sumofsquares and sum elements. If the window function proves useful, consider adding it here so that others can benefit.
It is convenient to describe the windows as functions on the normalized domain \(y \in [-1, 1]\). The window is zero outside this domain. The window functions defined in this package are as follows.
\begin{equation} w(y) = 1. \end{equation}
\begin{equation} w(y) = \cos^2 \frac{\pi}{2} y. \end{equation}
\begin{equation} w(y) = 1 - y^2. \end{equation}
\begin{equation} w(y) = 1 - |y|. \end{equation}
\begin{equation} w(y) = \left\{ \begin{array}{ll} 1 - 6 y^2 (1 - |y|) & |y| \leq 1 / 2, \\ 2 (1 - |y|)^3 & |y| > 1 / 2. \end{array}\right. \end{equation}
\begin{equation} w(y) = \frac{1}{\pi} \sin \pi |y| + (1 - |y|) \cos \pi |y|. \end{equation}
\begin{equation} w(y) = 0.08 + 0.92 \cos^{2} \frac{\pi}{2} y. \end{equation}
This is the same as the Hann window, but with an additional DC bias, or "foot," of 0.08.
\begin{equation} w(y) = I_0 \left( \beta \sqrt{1-y^2} \right) / I_0(\beta), \end{equation}
where \(I_0(x)\) is the \(0\)th order, modified Bessel function of the first kind. The shape parameter \(\beta \in [0, \infty]\) sets the sharpness of the central peak. \(\beta = 0\) yields the rectangle window, \(\beta \rightarrow \infty\) yields a \(\delta\) function with a single non-zero sample in the middle. This window is difficult to compute for large \(\beta\), and an asymptotic approximation is used for \(\beta \ge 705\). A linearly-interpolated transition occurs between \(\beta = 695\) and \(\beta = 705\). Finite-difference derivatives of the window with respect to \(\beta\) are unlikely to work well in this regime.
\begin{equation} w(y) = \exp \left( -\beta \frac{y^2}{1 - y^2} \right). \end{equation}
This window function is based on a fairly standard \(C_{\infty}\) test function used in distribution theory, e.g. Green's Functions and Boundary Value Problems [26] , by Stakgold. The shape parameter \(\beta \in [0, \infty]\) sets the sharpness of the central peak. \(\beta = 0\) yields the rectangle window, \(\beta \rightarrow \infty\) yields a \(\delta\) function with a single non-zero sample in the middle.
\begin{equation} w(y) = \left\{ \begin{array}{ll} \sin^2 \left[ \frac{\pi}{2} (|y| - 1) / \beta \right] & |y| \geq 1 - \beta, \\ 1 & |y| < 1 - \beta. \end{array} \right. \end{equation}
The shape parameter \(\beta \in [0, 1]\) sets what fraction of the window is spanned by the tapers. \(\beta = 0\) yields the rectangle window, \(\beta = 1\) yields the Hann window.
\begin{equation} w(y) = \exp \left( -\frac{1}{2} \beta^{2} y^{2} \right). \end{equation}
The shape parameter \(\beta \in [0, \infty]\) sets the sharpness of the central peak. \(\beta = 0\) yields the rectangle window, \(\beta \rightarrow \infty\) yields a \(\delta\) function with a single non-zero sample in the middle.
\begin{equation} w(y) = \frac{\sin \pi y}{\pi y}. \end{equation}
The Lanczos window is the central lobe of the sinc function. This is used, for example, in finite impulse response resampling to modulate a truncated sinc interpolating kernel.
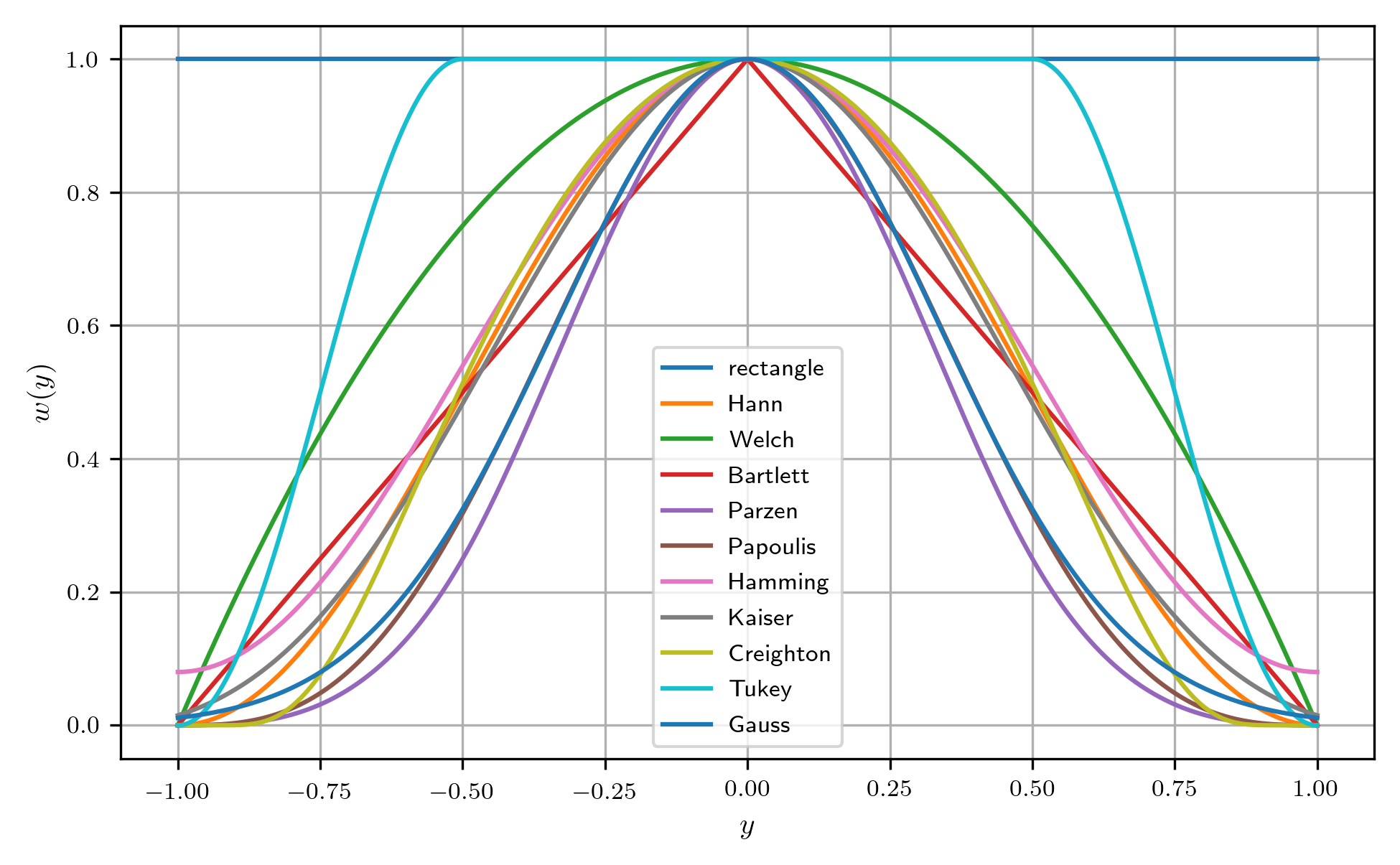
These window functions are shown in this figure, showing various windows as functions of the normalized independend variable \(y\), choosing \(\beta = 6\) for the Kaiser window, \(\beta = 2\) for the Creighton window, \(\beta = 0.5\) for the Tukey window, and \(\beta = 3\) for the Gauss window.
For a vector of length \(L\) (an integer), the mapping from integer array index \(i\) to normalized co-ordinate \(y\) is
\begin{equation} y(i) = \left\{ \begin{array}{ll} 0 & L \le 1, \\ 2 i / (L - 1) - 1 & L > 1, \end{array} \right. \end{equation}
where \(0 \le i < L\), and floating-point division is used. This agrees with J. G. Proakis and D. G. Manolakis, Digital Signal Processing [23] , and MatLab. The first sample is \(y = -1\), the last sample is \(y = +1\). For odd-lengthed vectors, the middle sample is \(y =
0\), while for even-lengthed vectors \(y = 0\) occurs half-way between the two middle samples. Substituting \(y(i)\) into the definitions of the window functions above yields \(w(i)\), the value of the window function at the integer sample \(i\).
The Fourier transforms of the windows are shown as functions of \(1 / y\) in this figure, showing frequency behaviour of various windows as functions of the inverse of the normalized independend variable \(y\), choosing \(\beta = 6\) for the Kaiser window, \(\beta = 2\) for the Creighton window, \(\beta = 0.5\) for the Tukey window, and \(\beta = 3\) for the Gauss window.

Since the Fourier transform of windowed data is the Fourier transform of the data convolved with the Fourier transform of the window, this figure is the major guideline for selecting a window. One can see that windows with a narrow central lobe tend to have higher sidelobes, and windows which suppress their low-order sidelobes tend to have more power in the high-order sidelobes. The choice of window thus depends on whether one is trying to resolve nearby spectral features of comparable magnitude (suggesting a rectangular or a Welch window), to reduce spectral bias and low-order sidelobes (a Hamming or Kaiser window), or to measure a broad spectrum with a large dynamical range (a Creighton or a Papoulis window).
Data Structures | |
| struct | REAL4Window |
| Structure for storing REAL4 window function data, providing storage for a sequence of samples as well as metadata about the window such as the sum-of-squarse of the samples. More... | |
| struct | REAL8Window |
| Structure for storing REAL8 window function data, providing storage for a sequence of samples as well as metadata about the window such as the sum-of-squarse of the samples. More... | |
| REAL4Window * XLALCreateREAL4WindowFromSequence | ( | REAL4Sequence * | sequence | ) |
Single-precision version of XLALCreateREAL8WindowFromSequence().
| REAL8Window * XLALCreateREAL8WindowFromSequence | ( | REAL8Sequence * | sequence | ) |
Constructs a new REAL8Window from a REAL8Sequence.
The window "owns" the sequence, when the window is destroyed the sequence will be destroyed with it. If this function fails, the sequence is destroyed. The return value is the address of the newly allocated REAL8Window or NULL on failure.
| REAL4Window * XLALCreateRectangularREAL4Window | ( | UINT4 | length | ) |
| REAL4Window * XLALCreateHannREAL4Window | ( | UINT4 | length | ) |
| REAL4Window * XLALCreateWelchREAL4Window | ( | UINT4 | length | ) |
| REAL4Window * XLALCreateBartlettREAL4Window | ( | UINT4 | length | ) |
| REAL4Window * XLALCreateParzenREAL4Window | ( | UINT4 | length | ) |
| REAL4Window * XLALCreatePapoulisREAL4Window | ( | UINT4 | length | ) |
| REAL4Window * XLALCreateHammingREAL4Window | ( | UINT4 | length | ) |
| REAL4Window * XLALCreateKaiserREAL4Window | ( | UINT4 | length, |
| REAL4 | beta | ||
| ) |
| REAL4Window * XLALCreateCreightonREAL4Window | ( | UINT4 | length, |
| REAL4 | beta | ||
| ) |
| REAL4Window * XLALCreateTukeyREAL4Window | ( | UINT4 | length, |
| REAL4 | beta | ||
| ) |
| REAL4Window * XLALCreateGaussREAL4Window | ( | UINT4 | length, |
| REAL4 | beta | ||
| ) |
| REAL4Window * XLALCreateLanczosREAL4Window | ( | UINT4 | length | ) |
| REAL8Window * XLALCreateRectangularREAL8Window | ( | UINT4 | length | ) |
| REAL8Window * XLALCreateHannREAL8Window | ( | UINT4 | length | ) |
| REAL8Window * XLALCreateWelchREAL8Window | ( | UINT4 | length | ) |
| REAL8Window * XLALCreateBartlettREAL8Window | ( | UINT4 | length | ) |
| REAL8Window * XLALCreateParzenREAL8Window | ( | UINT4 | length | ) |
| REAL8Window * XLALCreatePapoulisREAL8Window | ( | UINT4 | length | ) |
| REAL8Window * XLALCreateHammingREAL8Window | ( | UINT4 | length | ) |
| REAL8Window * XLALCreateKaiserREAL8Window | ( | UINT4 | length, |
| REAL8 | beta | ||
| ) |
| REAL8Window * XLALCreateCreightonREAL8Window | ( | UINT4 | length, |
| REAL8 | beta | ||
| ) |
| REAL8Window * XLALCreateTukeyREAL8Window | ( | UINT4 | length, |
| REAL8 | beta | ||
| ) |
| REAL8Window * XLALCreateGaussREAL8Window | ( | UINT4 | length, |
| REAL8 | beta | ||
| ) |
| REAL8Window * XLALCreateLanczosREAL8Window | ( | UINT4 | length | ) |
| void XLALDestroyREAL4Window | ( | REAL4Window * | window | ) |
| void XLALDestroyREAL8Window | ( | REAL8Window * | window | ) |
| REAL4Sequence * XLALUnitaryWindowREAL4Sequence | ( | REAL4Sequence * | sequence, |
| const REAL4Window * | window | ||
| ) |
Single-precision version of XLALUnitaryWindowREAL8Sequence().
| COMPLEX8Sequence * XLALUnitaryWindowCOMPLEX8Sequence | ( | COMPLEX8Sequence * | sequence, |
| const REAL4Window * | window | ||
| ) |
Single-precision complex version of XLALUnitaryWindowREAL8Sequence().
| REAL8Sequence * XLALUnitaryWindowREAL8Sequence | ( | REAL8Sequence * | sequence, |
| const REAL8Window * | window | ||
| ) |
Multiply a REAL8Sequence in-place by a REAL8Window with a normalization that preserves the variance of a zero-mean stationary Gaussian random process.
If the window's length is N samples and its sum-of-squares is S, then the input sequence is multiplied by the window * \(\sqrt{N / S}\). Returns the address of the REAL8Sequence or NULL on failure.
| COMPLEX16Sequence * XLALUnitaryWindowCOMPLEX16Sequence | ( | COMPLEX16Sequence * | sequence, |
| const REAL8Window * | window | ||
| ) |
Double-precision complex version of XLALUnitaryWindowREAL8Sequence().
| int XLALCheckNamedWindow | ( | const char * | windowName, |
| const BOOLEAN | haveBeta | ||
| ) |
| REAL8Window * XLALCreateNamedREAL8Window | ( | const char * | windowName, |
| REAL8 | beta, | ||
| UINT4 | length | ||
| ) |
| REAL4Window * XLALCreateNamedREAL4Window | ( | const char * | windowName, |
| REAL8 | beta, | ||
| UINT4 | length | ||
| ) |