Detailed Description

Functions to create a coarse grid of templates.

Author: Churches, D. K and Sathyaprakash, B.S.

The coarse grid algorithm works in two stages: After computing the minimum and maximum chirp-times corresponding to the search space: \((\tau_0^\mathrm{min}, \tau_0^\mathrm{max}),\) \((\tau_2^\mathrm{min}, \tau_2^\mathrm{max})\) (or [Note: In what follows we will only mention \(\tau_3\); however, the algorithm is itself valid, and has been implemented, in the case of \((\tau_0,\tau_2)\) too. However, we recommend that the space \(\tau_0\)- \(\tau_3\) be used.] \((\tau_3^\mathrm{min}, \tau_3^\mathrm{max})\)) the algorithm

chooses a lattice of templates along the equal mass curve and then
lays a rectangular grid in the rectangular region defined by the minimum and maximum values of the chirp-times and retain only if (a) the point lies in the parameter space, OR (b) one of the vertices defined by the rectangle lies in the parameter space.

Templates along the equal mass curve

The algorithm works in two stages: In the first stage, templates are built along the equal mass (that is, \(\eta=1/4\)) curve starting from the minimum value of the Newtonian chirp-time and stopping at its maximum value. Given the \(n\)\ th template at \(O\) with parameters \((\tau_0^{(n)},\tau_3^{(n)}),\) and given also the distance between templates in our preferred coordinates \((D\tau_0^{(n)},D\tau_3^{(n)}),\) consider lines \(\tau_0 = \tau_0^{(n)} + D\tau_0^{(n)}\) ( \(QA\) of this figure) and \(\tau_3 = \tau_3^{(n)} + D\tau_3^{(n)}\) ( \(PB\) of this figure).

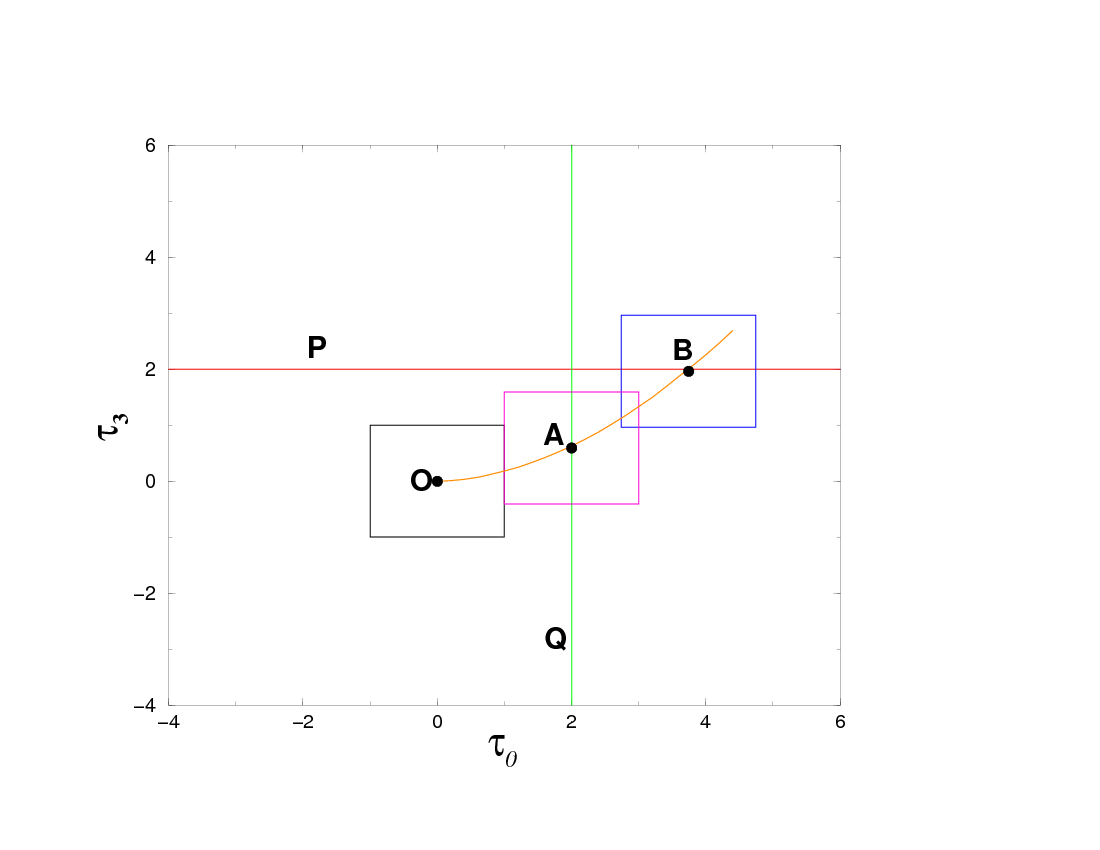
Algorithm sketching the placement of templates along eta=1/4 curve

The template next to \((\tau_0^{(n)},\tau_3^{(n)}),\) on the equal mass curve, must lie either along \(PB\) or along \(QA\) (cf. this figure in order that all the signals that may lie on \(OAB\) are spanned by at least one of the two templates. Clearly, if we were to place the \((n+1)\)\ th template at \(B,\) some of the signals won't have the required minimal match. However, placing the \((n+1)\)\ th template at \(A\) suffices our requirement. (Note, however, that there is no guarantee that this will always work; it works only if the curve along which templates are being laid is a slowly varying function.) To locate the \((n+1)\)\ th template we compute the following pairs of coordinates:

\begin{eqnarray} \tau_0^{(n+1)} = \tau_0^{(n)} + D\tau_0^{(n)}, \ \ \tau_3^{(n+1)} = 4A_3 \left ( \frac{\tau_0^{(n+1)}}{4A_0} \right )^{2/5} \\ \tau_3^{(n+1)} = \tau_3^{(n)} + D\tau_3^{(n)}, \ \ \tau_0^{(n+1)} = 4A_0 \left ( \frac{\tau_3^{(n+1)}}{4A_3} \right )^{5/2}, \end{eqnarray}

where

\begin{equation} A_0=\frac{5}{256 (\pi f_0)^{8/3}}, \ \ A_3=\frac{\pi}{8 (\pi f_0)^{5/3}}. \end{equation}

Of the two pairs, the required pair is the one that is closer to the starting point \((\tau_0^{(n)},\tau_3^{(n)}).\)

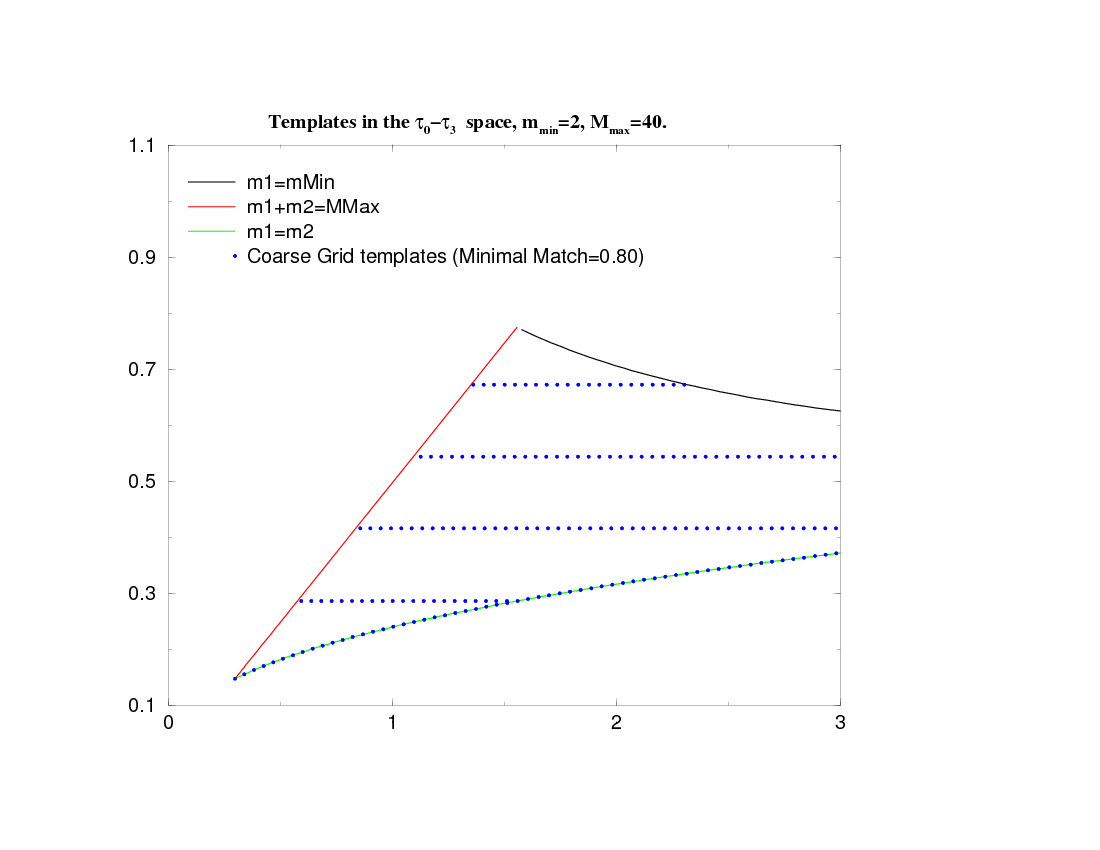
Templates in the rest of the parameter space

In the second stage, the algorithm begins again at the point \((\tau_0^\mathrm{min}, \tau_3^\mathrm{min}),\) corresponding distance between templates \((D\tau_0^\mathrm{min}, D\tau_3^\mathrm{min}),\) and chooses a rectangular lattice of templates in the rectangular region defined by \((\tau_0^\mathrm{min}, \tau_3^\mathrm{min})\) \((\tau_0^\mathrm{max}, \tau_3^\mathrm{min})\) \((\tau_0^\mathrm{max}, \tau_3^\mathrm{max})\) and \((\tau_0^\mathrm{min}, \tau_3^\mathrm{max})\). The implementation of the algorithm along the equal mass curve and in a rectangular lattice in the rest of the parameter space is shown plotted in this figure, where the templates chosen are represented as points.

Algorithm sketching the construction of a rectangular lattice of templates

Algorithm

The algorithm to lay templates along the equal-mass curve is as follows:



Begin at \(\tau_0 = \tau_0^\mathrm{min}\) 

do while \((\tau_0 < \tau_0^\mathrm{max})\)

 { 

\(\tau_0^A = \tau_0 + D\tau_0, \ \ \tau_3^A = 4A_3 \left ( {\tau_0^A}/{4A_0} \right )^{2/5}\) 

\(\tau_3^B = \tau_3 + D\tau_3, \ \ \tau_0^B = 4A_0 \left ( {\tau_3^B}/{4A_3} \right )^{5/2}\) 

if ( \((\tau_0^A,\tau_3^A)\) is closer \((\tau_0,\tau_3)\) than \((\tau_0^B,\tau_3^B)\))

 {

 \(\tau_0 = \tau_0^A, \tau_3 = \tau_3^A\)

 }

 

else 

 {

 \(\tau_0 = \tau_0^B, \tau_3 = \tau_3^B\) 

 }

 

Add \((\tau_0, \tau_3)\) to InspiralTemplateList 

numTemplates++ 

Compute metric at \((\tau_0, \tau_3)\) 

Compute distance between templates at new point: \((D\tau_0, D\tau_3)\) 

}

The algorithm to lay templates in the rest of the parameter space is as follows:



Begin at \(\tau_0 = \tau_0^\mathrm{min}, \tau_3 = \tau_3^\mathrm{min}\) 

Compute metric at \((\tau_0, \tau_3)\) 

Compute distance between templates at new point: \((D\tau_0, D\tau_3)\) 

Add \((\tau_0, \tau_3)\) to InspiralTemplateList 

numTemplates++ 

do while ( \(\tau_3 <= \tau_3^\mathrm{max}\))

 {

 

do while ( \(\tau_0 <= \tau_0^\mathrm{max}\))

 {

 

if ( \((\tau_0, \tau_3)\) is inside the parameter space)

 {

 

Compute metric at ( \(\tau_0, \tau_3\)) 

Compute distance between templates at new point: ( \(D\tau_0, D\tau_3\)) 

Add ( \(\tau_0, \tau_3\)) to InspiralTemplateList 

numTemplates++ 

}

 

Increment \(\tau_0:\) \(\tau_0 = \tau_0 + D\tau_0\)

 

}

 

Increment \(\tau_3:\) \(\tau_3 = \tau_3 + D\tau_3\) 

Get next template along \(\tau_3=\mathrm{const.}\): \((\tau_0, \tau_3)\)

 

}

Prototypes
void	LALInspiralCreateCoarseBank (LALStatus status, InspiralTemplateList list, INT4 nlist, InspiralCoarseBankIn coarseIn)

void	LALNudgeTemplatesToConstantTotalMassLine (LALStatus status, InspiralTemplateList *list, INT4 nlist, InspiralCoarseBankIn coarseIn)
	Anand: 26 October 2006 This function nudges the templates in the list to the (max-total-mass = constant) line. More...

void	LALInspiralCreatePNCoarseBank (LALStatus status, InspiralTemplateList list, INT4 nlist, InspiralCoarseBankIn coarseIn)

Function Documentation

◆ LALInspiralCreateCoarseBank()

void LALInspiralCreateCoarseBank	(	LALStatus *	status,
		InspiralTemplateList **	list,
		INT4 *	nlist,
		InspiralCoarseBankIn	coarseIn
	)

See also: See Module LALInspiralCreateCoarseBank.c for documentation

Parameters

	status	LAL-status pointer
[out]	list	an array containing the template bank parameters
[out]	nlist	the number of templates found by the function
[in]	coarseIn	specifies the search space, range of masses, etc

Definition at line 180 of file LALInspiralCreateCoarseBank.c.

◆ LALNudgeTemplatesToConstantTotalMassLine()

void LALNudgeTemplatesToConstantTotalMassLine	(	LALStatus *	status,
		InspiralTemplateList **	list,
		INT4	nlist,
		InspiralCoarseBankIn	coarseIn
	)

Anand: 26 October 2006 This function nudges the templates in the list to the (max-total-mass = constant) line.

This is done only for those templates whose total mass exceeds the desired max-total-mass value. The templates are nudged along the metric eigen direction until they lie on the said line.

Definition at line 298 of file LALInspiralCreateCoarseBank.c.

◆ LALInspiralCreatePNCoarseBank()

void LALInspiralCreatePNCoarseBank	(	LALStatus *	status,
		InspiralTemplateList **	list,
		INT4 *	nlist,
		InspiralCoarseBankIn	coarseIn
	)

See also: See Module LALInspiralCreateCoarseBank.c for documentation

Definition at line 407 of file LALInspiralCreateCoarseBank.c.