Detailed Description

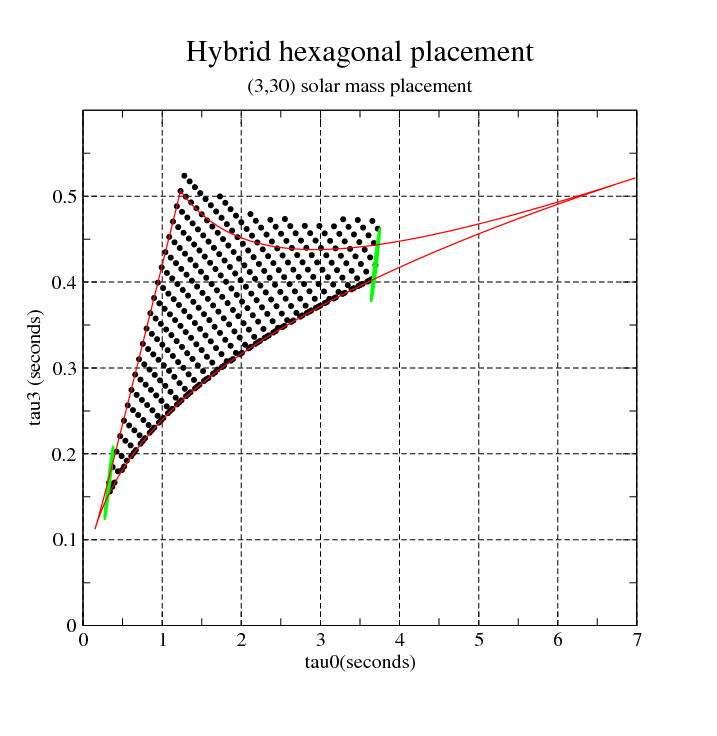
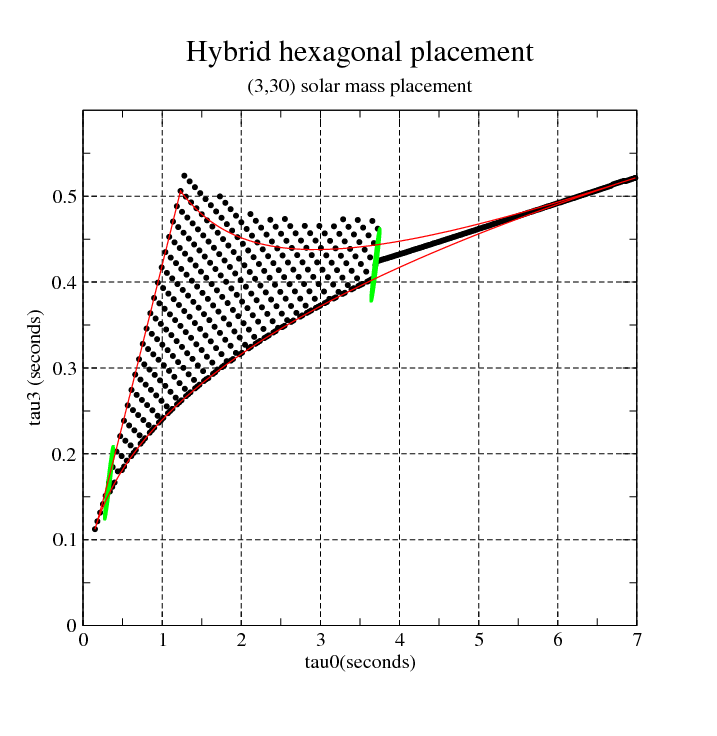
Hybrid hexagonal template bank.

Author: Cokelaer Thomas

Description

This code does almost the same as the standard Hexagonal Bank code. However, once the templates cover both the equal line and an other line ( \(m_1=\textrm{mMin}\) or \(m_2 =\textrm{mMax}\)), then there is no need to carry on any square/hexagonal placement. One can simply populate templates along a bissectrice.

Algorithm

The algorithm is identical to the hexagonal placement. However, once a template covers both the equal mass line and the upper boundary, then the hexagonal placement stops. So, an additional placement is needed to finalise the bank. In principle the placement needs to be completed on bothe side of the template bank, at low mass and high mass. So, we should start from the two templates which covers the two boundaries and populate the parameter space along a bissectrice.

The coordinates of the bissectrice at a given \(tau_0\) coordinate is estimated by tracing a vertical line in the \(\tau_0/tau_3\) plane, estimate the vlue of \(tau_3\) on the upper boundary and low boundary ( \(\eta=1/4\) line), and finally take the mean of the two values. Although, is is an approximation since we should also take into account the orientation of the ellipse, we think this is good enough. The vertical line crosses the parameter space on the \(\eta=1/4\) line and the other parameter space boundary which is define either by (1) \(m_1=variable\) and \(m_2=mMin\) or (2) \(m_1=variable\) and \(m_2=mMax\). Concerning (1), \(\eta=1/4\), this is a trivial computation, since

\begin{equation} \tau_3 = \frac{ A3}{\eta} \left( \frac{\eta \tau_0}{A0} \right)^{2/5}, \end{equation}

which in the case of \(\eta=1/4\) simply becomes :

\begin{equation} \tau_3 = 4 A3 \left( \frac{\tau_0}{4 A0} \right)^{2/5}. \end{equation}

In the case (2), if \(\tau_0\) is provided, if we can extract the total mass and \(\eta\) parameter, then \(tau_3\) is given by

\begin{equation} \tau_3 = \frac{ A3}{\eta} M^{-2/3}. \end{equation}

So, we need \(M\) and \(\eta\). Starting from

\begin{equation} \tau_0 = \frac{ A0}{\eta} \left( M \right)^{-5/3}, \end{equation}

we can extract a cubic equation

\begin{equation} x^3 - px+q=0 \end{equation}

where \(x = M^{1/3}\), \(p = -\frac{A0}{\tau_0/m_\textrm{Extreme}}\) and \(q= - m_\textrm{Extreme}=0\). \( m_\textrm{Extreme}\) is either set to mMin or mMax depending on which side of the parameter space we are.

The solution for \(x\) is standard and takes the expression :

\begin{equation} x = \left(-\frac{q}{2}-\frac{1}{2}*\sqrt{\frac{27 q^2 + 4 p^3}{27}}\right)^{\frac{1}{3}} + \left(-\frac{q}{2}+\frac{1}{2}*\sqrt{\frac{27 q^2 + 4 p^3}{27}}\right)^{\frac{1}{3}}; \end{equation}

Example of hybrid hexagonal placement. Once an ellipse covers the upper and lower boundary\, then the hexagonal placement stops. This occurs neccesseraly at low and high mass range.

Example of hybrid hexagonal placement. Once the ellipses covers the upper and lower part of the parameter space (at tau0=3.6 and tau0=0.4)\, then the placement is switched from the hexagonal to a placement along the bissectric of the upper/lower boundaries as described in the text.

Prototypes
void	LALPopulateNarrowEdge (LALStatus status, InspiralMomentsEtc moments, InspiralCell *cell, INT4 headId, InspiralTemplate paramsIn, HexaGridParam gridParam, CellEvolution cellEvolution, CellList **cellList, INT4 flag)

void	LALInspiralCreatePNCoarseBankHybridHexa (LALStatus status, InspiralTemplateList list, INT4 nlist, InspiralCoarseBankIn coarseIn)

REAL8	XLALInspiralBissectionLine (REAL8 tau0, REAL8 fL, REAL8 mMin, REAL8 mMax)

Function Documentation

◆ LALPopulateNarrowEdge()

void LALPopulateNarrowEdge	(	LALStatus *	status,
		InspiralMomentsEtc *	moments,
		InspiralCell **	cell,
		INT4	headId,
		InspiralTemplate *	paramsIn,
		HexaGridParam *	gridParam,
		CellEvolution *	cellEvolution,
		CellList **	cellList,
		INT4	flag
	)

See also: See Module LALInspiralHybridHexagonalBank.c for documentation

Definition at line 543 of file LALInspiralHybridHexagonalBank.c.

◆ LALInspiralCreatePNCoarseBankHybridHexa()

void LALInspiralCreatePNCoarseBankHybridHexa	(	LALStatus *	status,
		InspiralTemplateList **	list,
		INT4 *	nlist,
		InspiralCoarseBankIn	coarseIn
	)

See also: See Module LALInspiralHybridHexagonalBank.c for documentation

Definition at line 110 of file LALInspiralHybridHexagonalBank.c.

◆ XLALInspiralBissectionLine()

REAL8 XLALInspiralBissectionLine	(	REAL8	tau0,
		REAL8	fL,
		REAL8	mMin,
		REAL8	mMax
	)

See also: See Module LALInspiralHybridHexagonalBank.c for documentation

Definition at line 507 of file LALInspiralHybridHexagonalBank.c.