Fitting a model to data with both x and y errors with Bilby

Usually when we fit a model to data with a Gaussian Likelihood we assume that we know x values exactly. This is almost never the case. Here we show how to fit a model with errors in both x and y.

import bilby
import matplotlib.pyplot as plt
import numpy as np

%matplotlib inline

/opt/conda/envs/python310/lib/python3.10/site-packages/pandas/core/computation/expressions.py:21: UserWarning: Pandas requires version '2.8.4' or newer of 'numexpr' (version '2.7.3' currently installed).
  from pandas.core.computation.check import NUMEXPR_INSTALLED

Simulate data

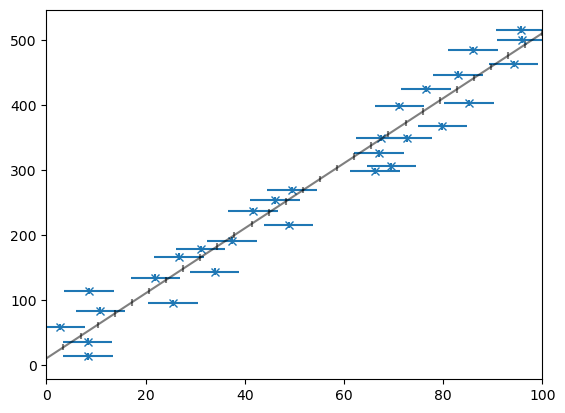
First we create the data and plot it

# define our model, a line
def model(x, m, c, **kwargs):
    y = m * x + c
    return y


# make a function to create and plot our data
def make_data(points, m, c, xerr, yerr, seed):
    np.random.seed(int(seed))
    xtrue = np.linspace(0, 100, points)
    ytrue = model(x=xtrue, m=m, c=c)

    xerr_vals = xerr * np.random.randn(points)
    yerr_vals = yerr * np.random.randn(points)
    xobs = xtrue + xerr_vals
    yobs = ytrue + yerr_vals

    plt.errorbar(xobs, yobs, xerr=xerr, yerr=yerr, fmt="x")
    plt.errorbar(xtrue, ytrue, yerr=yerr, color="black", alpha=0.5)
    plt.xlim(0, 100)
    plt.show()
    plt.close()

    data = {
        "xtrue": xtrue,
        "ytrue": ytrue,
        "xobs": xobs,
        "yobs": yobs,
        "xerr": xerr,
        "yerr": yerr,
    }

    return data


data = make_data(points=30, m=5, c=10, xerr=5, yerr=5, seed=123)

Define our prior and sampler settings

Now lets set up the prior and bilby output directory/sampler settings

# setting up bilby priors
priors = dict(
    m=bilby.core.prior.Uniform(0, 30, "m"), c=bilby.core.prior.Uniform(0, 30, "c")
)

sampler_kwargs = dict(priors=priors, sampler="bilby_mcmc", nsamples=1000, printdt=5, outdir="outdir", verbose=False, clean=True)

Fit with exactly known x-values

Our first step is to recover the straight line using a simple Gaussian Likelihood that only takes into account the y errors. Under the assumption we know x exactly. In this case, we pass in xtrue for x

known_x = bilby.core.likelihood.GaussianLikelihood(
    x=data["xtrue"], y=data["yobs"], func=model, sigma=data["yerr"]
)
result_known_x = bilby.run_sampler(
    likelihood=known_x,
    label="known_x",
    **sampler_kwargs,
)

04:49 bilby INFO    : Running for label 'known_x', output will be saved to 'outdir'

04:50 bilby INFO    : Analysis priors:

04:50 bilby INFO    : m=Uniform(minimum=0, maximum=30, name='m', latex_label='m', unit=None, boundary=None)

04:50 bilby INFO    : c=Uniform(minimum=0, maximum=30, name='c', latex_label='c', unit=None, boundary=None)

04:50 bilby INFO    : Analysis likelihood class: <class 'bilby.core.likelihood.GaussianLikelihood'>

04:50 bilby INFO    : Analysis likelihood noise evidence: nan

04:50 bilby INFO    : Single likelihood evaluation took nan s

04:50 bilby INFO    : Using sampler Bilby_MCMC with kwargs {'nsamples': 1000, 'nensemble': 1, 'pt_ensemble': False, 'ntemps': 1, 'Tmax': None, 'Tmax_from_SNR': 20, 'initial_betas': None, 'adapt': True, 'adapt_t0': 100, 'adapt_nu': 10, 'pt_rejection_sample': False, 'burn_in_nact': 10, 'thin_by_nact': 1, 'fixed_discard': 0, 'autocorr_c': 5, 'L1steps': 100, 'L2steps': 3, 'printdt': 5, 'check_point_delta_t': 1800, 'min_tau': 1, 'proposal_cycle': 'default', 'stop_after_convergence': False, 'fixed_tau': None, 'tau_window': None, 'evidence_method': 'stepping_stone', 'initial_sample_method': 'prior', 'initial_sample_dict': None}

04:50 bilby INFO    : Initializing BilbyPTMCMCSampler with:
  Convergence settings: ConvergenceInputs(autocorr_c=5, burn_in_nact=10, thin_by_nact=1, fixed_discard=0, target_nsamples=1000, stop_after_convergence=False, L1steps=100, L2steps=3, min_tau=1, fixed_tau=None, tau_window=None)
  Parallel-tempering settings: ParallelTemperingInputs(ntemps=1, nensemble=1, Tmax=None, Tmax_from_SNR=20, initial_betas=None, adapt=True, adapt_t0=100, adapt_nu=10, pt_ensemble=False)
  proposal_cycle: default
  pt_rejection_sample: False

04:50 bilby INFO    : Setting parallel tempering inputs=ParallelTemperingInputs(ntemps=1, nensemble=1, Tmax=None, Tmax_from_SNR=20, initial_betas=None, adapt=True, adapt_t0=100, adapt_nu=10, pt_ensemble=False)

04:50 bilby INFO    : Initializing BilbyPTMCMCSampler with:ntemps=1, nensemble=1, pt_ensemble=False, initial_betas=[1], initial_sample_method=prior, initial_sample_dict=None

04:50 bilby INFO    : Using initial sample {'m': 26.71740826551804, 'c': 1.6916325823002654}

04:50 bilby INFO    : Using ProposalCycle:
  AdaptiveGaussianProposal(acceptance_ratio:nan,n:0,scale:1,)
  DifferentialEvolutionProposal(acceptance_ratio:nan,n:0,)
  UniformProposal(acceptance_ratio:nan,n:0,)
  KDEProposal(acceptance_ratio:nan,n:0,trained:0,)
  FisherMatrixProposal(acceptance_ratio:nan,n:0,scale:1,)
  GMMProposal(acceptance_ratio:nan,n:0,trained:0,)

04:50 bilby INFO    : Setting convergence_inputs=ConvergenceInputs(autocorr_c=5, burn_in_nact=10, thin_by_nact=1, fixed_discard=0, target_nsamples=1000, stop_after_convergence=False, L1steps=100, L2steps=3, min_tau=1, fixed_tau=None, tau_window=None)

04:50 bilby INFO    : Drawing 1000 samples

04:50 bilby INFO    : Checkpoint every check_point_delta_t=1800s

04:50 bilby INFO    : Print update every printdt=5s

04:50 bilby INFO    : Reached convergence: exiting sampling

04:50 bilby INFO    : Checkpoint start

04:50 bilby INFO    : Written checkpoint file outdir/known_x_resume.pickle

04:50 bilby INFO    : Zero-temperature proposals:

04:50 bilby INFO    : AdaptiveGaussianProposal(acceptance_ratio:0.23,n:2.8e+04,scale:0.0049,)

04:50 bilby INFO    : DifferentialEvolutionProposal(acceptance_ratio:0.47,n:2.6e+04,)

04:50 bilby INFO    : UniformProposal(acceptance_ratio:1,n:1.7e+03,)

04:50 bilby INFO    : KDEProposal(acceptance_ratio:0.00014,n:2.9e+04,trained:0,)

04:50 bilby INFO    : FisherMatrixProposal(acceptance_ratio:0.56,n:2.6e+04,scale:1,)

04:50 bilby INFO    : GMMProposal(acceptance_ratio:0,n:3.1e+04,trained:0,)

04:50 bilby INFO    : Current taus={'m': 1, 'c': 1}

04:50 bilby INFO    : Creating diagnostic plots

04:50 bilby INFO    : Checkpoint finished

04:50 bilby INFO    : Sampling time: 0:00:15.017339

04:50 bilby INFO    : Summary of results:
nsamples: 1306
ln_noise_evidence:    nan
ln_evidence:    nan +/-    nan
ln_bayes_factor:    nan +/-    nan

_ = result_known_x.plot_corner(truth=dict(m=5, c=10), titles=True, save=False)
plt.show()
plt.close()

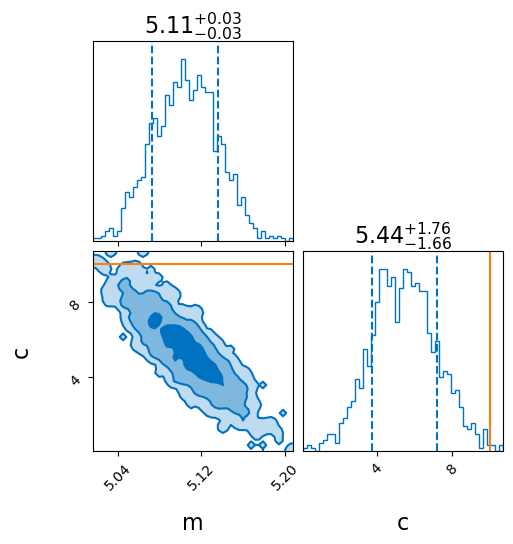
Fit with unmodeled uncertainty in the x-values

As expected this is easy to recover and the sampler does a good job. However this was made too easy - by passing in the ‘true’ values of x. Lets see what happens when we pass in the observed values of x

incorrect_x = bilby.core.likelihood.GaussianLikelihood(
    x=data["xobs"], y=data["yobs"], func=model, sigma=data["yerr"]
)
result_incorrect_x = bilby.run_sampler(
    likelihood=incorrect_x,
    label="incorrect_x",
    **sampler_kwargs,
)

04:50 bilby INFO    : Running for label 'incorrect_x', output will be saved to 'outdir'

04:50 bilby INFO    : Analysis priors:

04:50 bilby INFO    : m=Uniform(minimum=0, maximum=30, name='m', latex_label='m', unit=None, boundary=None)

04:50 bilby INFO    : c=Uniform(minimum=0, maximum=30, name='c', latex_label='c', unit=None, boundary=None)

04:50 bilby INFO    : Analysis likelihood class: <class 'bilby.core.likelihood.GaussianLikelihood'>

04:50 bilby INFO    : Analysis likelihood noise evidence: nan

04:50 bilby INFO    : Single likelihood evaluation took nan s

04:50 bilby INFO    : Using sampler Bilby_MCMC with kwargs {'nsamples': 1000, 'nensemble': 1, 'pt_ensemble': False, 'ntemps': 1, 'Tmax': None, 'Tmax_from_SNR': 20, 'initial_betas': None, 'adapt': True, 'adapt_t0': 100, 'adapt_nu': 10, 'pt_rejection_sample': False, 'burn_in_nact': 10, 'thin_by_nact': 1, 'fixed_discard': 0, 'autocorr_c': 5, 'L1steps': 100, 'L2steps': 3, 'printdt': 5, 'check_point_delta_t': 1800, 'min_tau': 1, 'proposal_cycle': 'default', 'stop_after_convergence': False, 'fixed_tau': None, 'tau_window': None, 'evidence_method': 'stepping_stone', 'initial_sample_method': 'prior', 'initial_sample_dict': None}

04:50 bilby INFO    : Initializing BilbyPTMCMCSampler with:
  Convergence settings: ConvergenceInputs(autocorr_c=5, burn_in_nact=10, thin_by_nact=1, fixed_discard=0, target_nsamples=1000, stop_after_convergence=False, L1steps=100, L2steps=3, min_tau=1, fixed_tau=None, tau_window=None)
  Parallel-tempering settings: ParallelTemperingInputs(ntemps=1, nensemble=1, Tmax=None, Tmax_from_SNR=20, initial_betas=None, adapt=True, adapt_t0=100, adapt_nu=10, pt_ensemble=False)
  proposal_cycle: default
  pt_rejection_sample: False

04:50 bilby INFO    : Setting parallel tempering inputs=ParallelTemperingInputs(ntemps=1, nensemble=1, Tmax=None, Tmax_from_SNR=20, initial_betas=None, adapt=True, adapt_t0=100, adapt_nu=10, pt_ensemble=False)

04:50 bilby INFO    : Initializing BilbyPTMCMCSampler with:ntemps=1, nensemble=1, pt_ensemble=False, initial_betas=[1], initial_sample_method=prior, initial_sample_dict=None

04:50 bilby INFO    : Using initial sample {'m': 3.8321032421915167, 'c': 26.15152772540474}

04:50 bilby INFO    : Using ProposalCycle:
  AdaptiveGaussianProposal(acceptance_ratio:nan,n:0,scale:1,)
  DifferentialEvolutionProposal(acceptance_ratio:nan,n:0,)
  UniformProposal(acceptance_ratio:nan,n:0,)
  KDEProposal(acceptance_ratio:nan,n:0,trained:0,)
  FisherMatrixProposal(acceptance_ratio:nan,n:0,scale:1,)
  GMMProposal(acceptance_ratio:nan,n:0,trained:0,)

04:50 bilby INFO    : Setting convergence_inputs=ConvergenceInputs(autocorr_c=5, burn_in_nact=10, thin_by_nact=1, fixed_discard=0, target_nsamples=1000, stop_after_convergence=False, L1steps=100, L2steps=3, min_tau=1, fixed_tau=None, tau_window=None)

04:50 bilby INFO    : Drawing 1000 samples

04:50 bilby INFO    : Checkpoint every check_point_delta_t=1800s

04:50 bilby INFO    : Print update every printdt=5s

04:50 bilby INFO    : Reached convergence: exiting sampling

04:50 bilby INFO    : Checkpoint start

04:50 bilby INFO    : Written checkpoint file outdir/incorrect_x_resume.pickle

04:50 bilby INFO    : Zero-temperature proposals:

04:50 bilby INFO    : AdaptiveGaussianProposal(acceptance_ratio:0.23,n:2.8e+04,scale:0.0035,)

04:50 bilby INFO    : DifferentialEvolutionProposal(acceptance_ratio:0.46,n:2.7e+04,)

04:50 bilby INFO    : UniformProposal(acceptance_ratio:1,n:1.4e+03,)

04:50 bilby INFO    : KDEProposal(acceptance_ratio:3.2e-05,n:3.1e+04,trained:0,)

04:50 bilby INFO    : FisherMatrixProposal(acceptance_ratio:0.55,n:2.6e+04,scale:1,)

04:50 bilby INFO    : GMMProposal(acceptance_ratio:7.6e-05,n:2.6e+04,trained:0,)

04:50 bilby INFO    : Current taus={'m': 1.0, 'c': 1}

04:50 bilby INFO    : Creating diagnostic plots

04:50 bilby INFO    : Checkpoint finished

04:50 bilby INFO    : Sampling time: 0:00:15.014865

04:50 bilby INFO    : Summary of results:
nsamples: 1288
ln_noise_evidence:    nan
ln_evidence:    nan +/-    nan
ln_bayes_factor:    nan +/-    nan

_ = result_incorrect_x.plot_corner(truth=dict(m=5, c=10), titles=True, save=False)
plt.show()
plt.close()

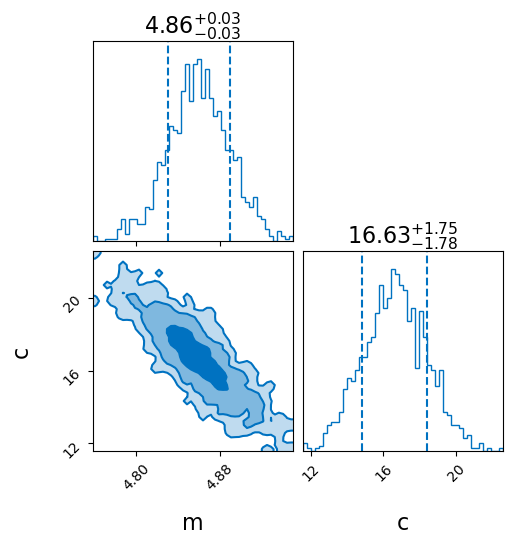
Fit with modeled uncertainty in x-values

This is not good as there is unmodelled uncertainty in our x values. Getting around this requires marginalisation of the true x values or sampling over them. See discussion in section 7 of https://arxiv.org/pdf/1008.4686.pdf.

For this, we will have to define a new likelihood class. By subclassing the base bilby.core.likelihood.Likelihood class we can do this fairly simply.

class GaussianLikelihoodUncertainX(bilby.core.likelihood.Likelihood):
    def __init__(self, xobs, yobs, xerr, yerr, function):
        """

        Parameters
        ----------
        xobs, yobs: array_like
            The data to analyse
        xerr, yerr: array_like
            The standard deviation of the noise
        function:
            The python function to fit to the data
        """
        super(GaussianLikelihoodUncertainX, self).__init__(dict())
        self.xobs = xobs
        self.yobs = yobs
        self.yerr = yerr
        self.xerr = xerr
        self.function = function

    def log_likelihood(self):
        variance = (self.xerr * self.parameters["m"]) ** 2 + self.yerr**2
        model_y = self.function(self.xobs, **self.parameters)
        residual = self.yobs - model_y

        ll = -0.5 * np.sum(residual**2 / variance + np.log(variance))

        return -0.5 * np.sum(residual**2 / variance + np.log(variance))

gaussian_unknown_x = GaussianLikelihoodUncertainX(
    xobs=data["xobs"],
    yobs=data["yobs"],
    xerr=data["xerr"],
    yerr=data["yerr"],
    function=model,
)
result_unknown_x = bilby.run_sampler(
    likelihood=gaussian_unknown_x,
    label="unknown_x",
    **sampler_kwargs,
)

04:50 bilby INFO    : Running for label 'unknown_x', output will be saved to 'outdir'

04:50 bilby INFO    : Analysis priors:

04:50 bilby INFO    : m=Uniform(minimum=0, maximum=30, name='m', latex_label='m', unit=None, boundary=None)

04:50 bilby INFO    : c=Uniform(minimum=0, maximum=30, name='c', latex_label='c', unit=None, boundary=None)

04:50 bilby INFO    : Analysis likelihood class: <class '__main__.GaussianLikelihoodUncertainX'>

04:50 bilby INFO    : Analysis likelihood noise evidence: nan

04:50 bilby INFO    : Single likelihood evaluation took nan s

04:50 bilby INFO    : Using sampler Bilby_MCMC with kwargs {'nsamples': 1000, 'nensemble': 1, 'pt_ensemble': False, 'ntemps': 1, 'Tmax': None, 'Tmax_from_SNR': 20, 'initial_betas': None, 'adapt': True, 'adapt_t0': 100, 'adapt_nu': 10, 'pt_rejection_sample': False, 'burn_in_nact': 10, 'thin_by_nact': 1, 'fixed_discard': 0, 'autocorr_c': 5, 'L1steps': 100, 'L2steps': 3, 'printdt': 5, 'check_point_delta_t': 1800, 'min_tau': 1, 'proposal_cycle': 'default', 'stop_after_convergence': False, 'fixed_tau': None, 'tau_window': None, 'evidence_method': 'stepping_stone', 'initial_sample_method': 'prior', 'initial_sample_dict': None}

04:50 bilby INFO    : Initializing BilbyPTMCMCSampler with:
  Convergence settings: ConvergenceInputs(autocorr_c=5, burn_in_nact=10, thin_by_nact=1, fixed_discard=0, target_nsamples=1000, stop_after_convergence=False, L1steps=100, L2steps=3, min_tau=1, fixed_tau=None, tau_window=None)
  Parallel-tempering settings: ParallelTemperingInputs(ntemps=1, nensemble=1, Tmax=None, Tmax_from_SNR=20, initial_betas=None, adapt=True, adapt_t0=100, adapt_nu=10, pt_ensemble=False)
  proposal_cycle: default
  pt_rejection_sample: False

04:50 bilby INFO    : Setting parallel tempering inputs=ParallelTemperingInputs(ntemps=1, nensemble=1, Tmax=None, Tmax_from_SNR=20, initial_betas=None, adapt=True, adapt_t0=100, adapt_nu=10, pt_ensemble=False)

04:50 bilby INFO    : Initializing BilbyPTMCMCSampler with:ntemps=1, nensemble=1, pt_ensemble=False, initial_betas=[1], initial_sample_method=prior, initial_sample_dict=None

04:50 bilby INFO    : Using initial sample {'m': 8.938728536283739, 'c': 24.292869621251317}

04:50 bilby INFO    : Using ProposalCycle:
  AdaptiveGaussianProposal(acceptance_ratio:nan,n:0,scale:1,)
  DifferentialEvolutionProposal(acceptance_ratio:nan,n:0,)
  UniformProposal(acceptance_ratio:nan,n:0,)
  KDEProposal(acceptance_ratio:nan,n:0,trained:0,)
  FisherMatrixProposal(acceptance_ratio:nan,n:0,scale:1,)
  GMMProposal(acceptance_ratio:nan,n:0,trained:0,)

04:50 bilby INFO    : Setting convergence_inputs=ConvergenceInputs(autocorr_c=5, burn_in_nact=10, thin_by_nact=1, fixed_discard=0, target_nsamples=1000, stop_after_convergence=False, L1steps=100, L2steps=3, min_tau=1, fixed_tau=None, tau_window=None)

04:50 bilby INFO    : Drawing 1000 samples

04:50 bilby INFO    : Checkpoint every check_point_delta_t=1800s

04:50 bilby INFO    : Print update every printdt=5s

04:51 bilby INFO    : Reached convergence: exiting sampling

04:51 bilby INFO    : Checkpoint start

04:51 bilby INFO    : Written checkpoint file outdir/unknown_x_resume.pickle

04:51 bilby INFO    : Zero-temperature proposals:

04:51 bilby INFO    : AdaptiveGaussianProposal(acceptance_ratio:0.23,n:2.8e+04,scale:0.013,)

04:51 bilby INFO    : DifferentialEvolutionProposal(acceptance_ratio:0.47,n:2.9e+04,)

04:51 bilby INFO    : UniformProposal(acceptance_ratio:1,n:1.5e+03,)

04:51 bilby INFO    : KDEProposal(acceptance_ratio:0.0012,n:2.7e+04,trained:0,)

04:51 bilby INFO    : FisherMatrixProposal(acceptance_ratio:0.52,n:2.7e+04,scale:1,)

04:51 bilby INFO    : GMMProposal(acceptance_ratio:0.00093,n:2.9e+04,trained:0,)

04:51 bilby INFO    : Current taus={'m': 1.0, 'c': 1}

04:51 bilby INFO    : Creating diagnostic plots

04:51 bilby INFO    : Checkpoint finished

04:51 bilby INFO    : Sampling time: 0:00:15.016020

04:51 bilby INFO    : Summary of results:
nsamples: 1315
ln_noise_evidence:    nan
ln_evidence:    nan +/-    nan
ln_bayes_factor:    nan +/-    nan

_ = result_unknown_x.plot_corner(truth=dict(m=5, c=10), titles=True, save=False)
plt.show()
plt.close()

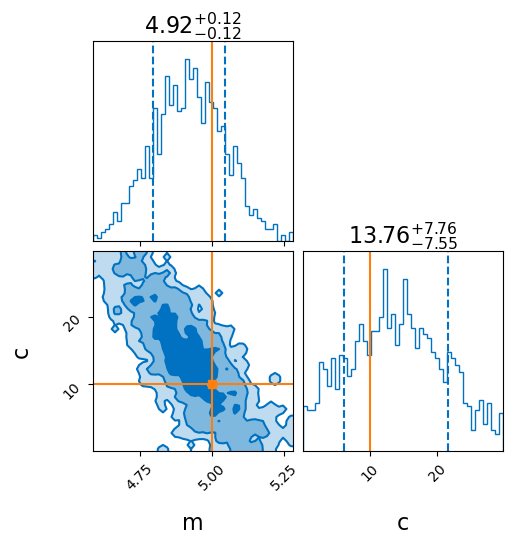
Success! The inferred posterior is consistent with the true values.